My Not-So-Hyper Loop
(Some TL;DR love: What I’m going to talk about is a variation on a Gravity Train. )
Ah, the Hyperloop. Holy crap, it even has its own Wikipedia page.
If you have no idea what I’m talking about, that’s okay. No one else does either. Which is why I’m writing this post. Something as vague and amorphous as the Hyperloop brings out all of the kooks and the cranks, including Yours Truly. This whole episode reminds me very much of the “Ginger” hysteria from 2001.
I have no better idea than you what the damned thing is. All I know is that listening to Elon describe it, it started to sound like a crackpot idea I had many years ago. Ordinarily I keep my mouth shut about such things (high school taught me that), but every now and then it’s fun to share a goofy idea and this seems like a great time to do it. Ready? Cool!
Uh… so… this is where you flat-Earthers are going to get really pissed. Sorry. Here’s a diagram of the Earth:
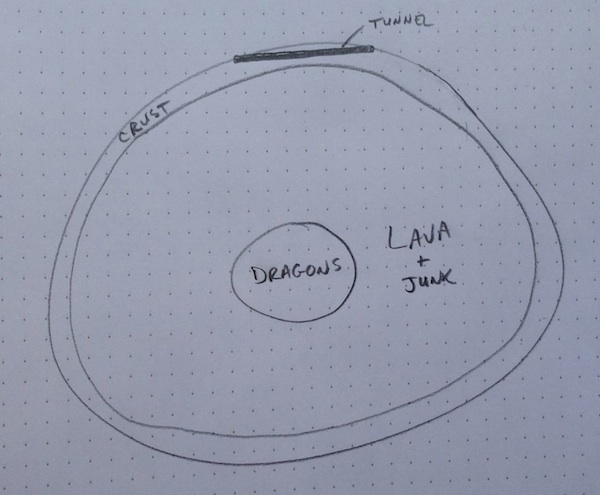
Yeah, I know. Art school really paid off.
The Earth has this curve to it, you know? And if you make a straight tunnel long enough, eventually you’re going to come out the other side. If you shoot straight through the planet you’ll hit molten lava or something. Not awesome. But if you limit the distance you’re trying to go, your tunnel can stay safely inside the earth’s crust, as shown.
Elon talked specifically about a connection between Los Angeles and San Francisco, so let’s draw that:
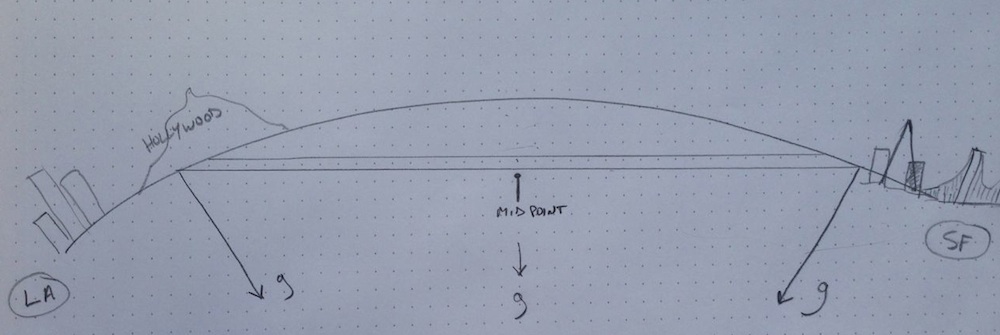
Aside from the startling reality of the drawing, you’ll notice some arrows labeled ‘g’. Those indicate the direction that gravity is pulling from different points along the tunnel.
(For some reason the tunnel I drew extends from the Hollywood hills to somewhere around the Mission District.)
What’s awesome about this tunnel is that it is downhill from both sides. If you are wondering how a tunnel can be downhill both ways, imagine walking through the tunnel in the picture. At first, it’s downhill. As you walk further, the tunnel has a different angle relative to the Earth’s center of gravity. Over more and more distance the angle changes enough that by the middle of the tunnel things are flat, neither downhill or uphill. Gravity is pulling straight down. Then as you continue forward it’s uphill to the other end of the tunnel. While the tunnel seems like a straight line to you, from the perspective of gravity it is shaped more like a half-pipe. In other words, the tunnel is downhill at both ends and is uphill in both directions from the middle. As Einstein once said, “Gravity be crazy, yo!”[1]
Anyway, I had the basic idea for a tunnel that you could hurl things through. There were some things I wanted to know. Namely:
- Would the tunnel stay inside the Earth’s crust?
- How fast could you go, with no additional energy, ignoring friction?
- How long would a trip take, with no additional energy, ignoring friction?
It’s about time we had a diagram.
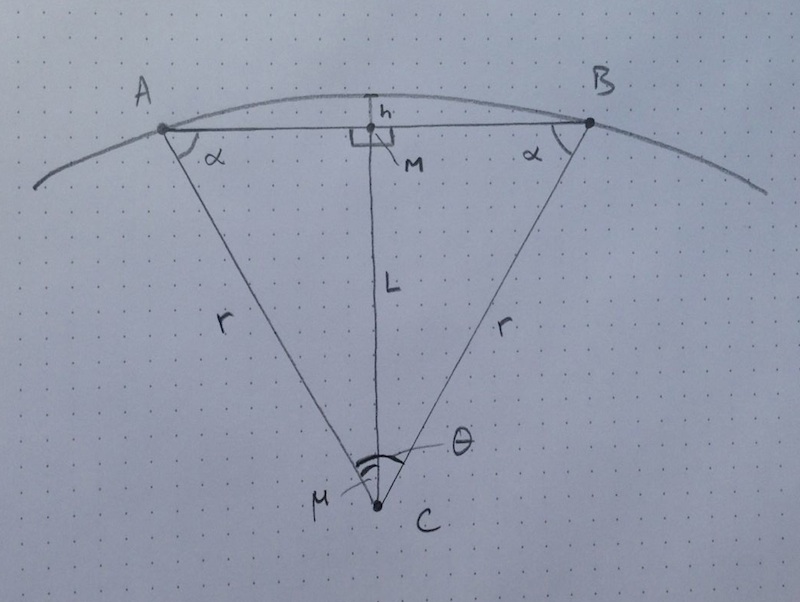
Of course this is just a conceptual diagram to help think about the problem. The Earth is HUGE and this triangle would be absurdly narrow and deep if we tried to keep things scaled in any way to reality.
The Details
Remember that part about Earth having a curve to it? That turns out to be a bit of a hassle. The curve is important to this problem, but the Earth doesn’t have the same curve everywhere. Seriously, this is the kind of thing people write dissertations about. After many rounds of trying to get super-accurate numbers, I opted to go with “cocktail napkin”-quality calculations. This means I’m using the median radius value of Earth that I found online, not the actual value for the region between LA and SF. Since this is not a project proposal and I am just some random guy on the Internet with a blog, I hope you’ll allow me this indulgence. My calculations are in the notes below, after the end of the post.
The key piece of information I wanted to know was ‘h’, the depth of the tunnel at the mid-point. That is because I wanted to know how fast you’d go if you were to slide down this tunnel through the mid-point. I also wanted to know if this tunnel would stay within the Earth’s crust over its entire length.
The number I came up with was about 6 km. That’s deeper than I expected. The Earth’s crust turns out to be between 5 km to 70 km thick depending on where you are. Since I know absolutely nothing about geology, I’m just going to pretend that the crust is substantially thicker than 6 km in the LA to SF area.
Honestly, given this “median radius” I’m working with, I wouldn’t be surprised if my numbers are way off. Earlier numbers, where I was trying to be more accurate, put the depth at more like 2 km which is borderline practical. It’s also way more boring, because the greater the depth, the faster we can go…
The depth of the tunnel’s mid-point tells us the velocity for any mass allowed to fall into the tunnel. This is in an imaginary scenario where there is no friction or air resistance and no energy is added to the system. The mass is just “dropped” down the tunnel. At first you’d start off slow, heading down a 4% grade, but my numbers say that you’d be going about 767 mph (~ 1234.5 kph, interestingly) by the time you reached the mid-point of the tunnel. That’s around the speed of sound. It’s also in the neighborhood of “twice as fast as a plane”, if you consider typical commercial airspeeds.
I did not end up calculating the trip time. See “Problems” and the calculation notes for more on that.
Interesting Properties of Tunnels
Tunnels are “immune to weather”.
Tunnels work well with maglev. I built a model maglev train for a project in grade school. It didn’t work too well. My cars wouldn’t stay on the track. The permanent magnets I was using would flip my cars over. In a tunnel that doesn’t have to happen – you have more surface to use than just the ground.
If you build your conveyance (space pod, trolley, what have you – I’ll use “car”) to work with the tunnel you can have something that never derails. Further, despite those action movies where people dive out of airplanes to save other people who were thrown out of airplanes, falling bodies tend to fall with uniform motion. That is to say, if you pushed a car down this tunnel and then pushed another one down the tunnel shortly afterward, they “never crash” into each other because they’re following the same path and obey the same laws of motion. The number of cars you could have in the tunnel at any one time is determined by the length of the tunnel. If you had a tunnel going in each direction you could keep a continuous loop going so “there is no waiting for a specific departure time”.
Problems
A few times above I oddly quoted a term or phrase. Those were various descriptions that Elon has used. Just because something matches a description doesn’t mean it’s the same though. Only some of this comparison stands up to close scrutiny. Particularly problematic is the matter of speed. I haven’t calculated the total trip time yet but the only way I could get my trip time under 30 mins is if the average speed for the entire trip was the maximum speed I calculated at the mid-point of the tunnel. (For the curious, the trip at that maximum speed would be about 27 minutes, “under 30 minutes”). Also, friction and air resistance are things that I’ve completely ignored. The final major problem is cost. He has estimated a $6B project cost. Can you tunnel nearly 550km on $6B? Maybe. I really don’t know.
OTOH
This whole scheme I’ve described is based on zero external energy and zero initial velocity when cars enter the tunnel. When you add in the costs of friction (even if you do maglev) you have to have some kind of external energy source to at least make up for the losses. And if you’re going to add extra energy to the system, you might as well add enough to make it interesting. Maybe even get the speed up and bring the travel time down. I’ve heard some people talk about rail guns. That sounds interesting.
Oh, and one other thing I can’t help but point out: Elon used the phrase “average speed”. You either raised your eyebrows at that or you didn’t. I know I did.
What’s the Point of All of This? Is This the Hyperloop?
Wouldn’t that be awesome? But no, I’m sure I’m way off the mark. After all, I thought “Ginger” was going to be a flying car or jetpack. You know, something cool. For the Hyperloop, the similarities to my idea were too good to pass up. I had to make the comparison. There are probably dozens of other unrelated schemes that could fit the description Elon’s given so far.
I guess the point is that we can all dream up interesting ideas, and we should play with those ideas more, even if we’re not Tony Stark. I used to do this all the time when I was 11 or 12 years old. Why don’t I do that anymore? Playing around with this has been fun!
(A nice conversation about this has popped up in a friend’s Google+ stream.)
[1] Or maybe it was Heisenberg’s lab assistant?
—-
Cocktail Napkin Calculations
The numbers I started with (all figures approximate):
| Surface distance between SF and LA | s = | 550 km |
| Median radius of the Earth | r = | 6372 km |
Find h:
h = r – L
To find L, I needed to know μ, and to know μ I needed to know θ, which is the angle between the two cities from the perspective of the center of the Earth. This is where having super-accurate curve info would have been handy. But oh well, on we go with the median radius.
θ = s/r = 0.0863 radians = 4.945 degrees
μ = 0.5 θ = 2.47 degrees
L = r * cos μ = 6366 km
h = r – L = 6372 – 6366 = 6 km
—
Maximum velocity v:
v = sqrt(2gh) = sqrt( 2 * 9.8 m/s/s * 6000 m) = 342.9 m/s = 1234 km/h = 767 mph
—
Time for trip if at max velocity: t = 550 km / (1234 km/h) = 0.445 h = 26.7 mins
—
Slope of the tunnel at each end would also be 2.47 degrees.
Grade = tan(2.47) * 100 = 4.31%
—-
I’ve ignored the gravity of the portion of earth above the tunnel. The ideal shape would probably have some curve to it. Speaking of which, “hypocycloid” sounds a lot like “hyperloop”. Coincidence? Probably.
—
I didn’t calculate the travel time through the tunnel because the angle of gravity changes as you go which is different than a first-year physics velocity calculation where g is always straight down. This started to look like a path integral so I ran away! The Gravity Train article suggests that on Earth this time is always 42 minutes, but I’m not convinced that this is the same problem, as the gravity train notion involves taking some optimal path deep through the earth. Clearly, I have homework to do. If there’s an easier solution or you’re handy at this kind of thing, get in touch. Thanks.
Update: Alan Eliasen, creator of the lovely Frink programming language, shared a program that calculates point-to-point travel times through a more realistic model of the Earth. He’s seeing a 38 minute travel time rather than 42.
